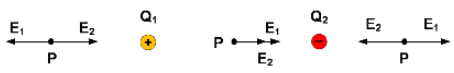Pembahasan
Diketahui :
Ditanya :
Tentukan letak titik yang memiliki kuat medan listrik nol?
Jawab :
Arah medan listrik pada muatan positif adalah keluar dan arah medan listrik pada muatan negatif adalah masuk.
Langkah 1, menentukan letak titik P.
Letak titik belum diketahui sehingga ada tiga kemungkinan yaitu di seblah kiri Q1, di sebelah kanan Q2 atau diantara Q1 dan Q2. Untuk memilih posisinya secara benar perhatikan ilustrasi berikut ini dan ingat kembali bahwa kuat medan listrik “keluar untuk muatan positif” dan “masuk untuk muatan negatif”. Namakan saja titik yang akan dicari sebagai titik P.
Ada 2 tempat dimana E1 dan E2 saling berlawanan, ambil saja titik yang lebih dekat dengan muatan yang nilai mutlaknya lebih kecil yaitu disebelah kiri Q1 dan namakan jaraknya sebagai x. Sehingga kita dapat menentukan jarak antara Q1 dan titik P (r1P = x), serta jarak antara muatan Q2 dan titik P (r2P = 10 + x).
Langkah 2, menghitung letak titik P yang mempunyai kuat medan listrik nol.
Syarat agar listrik di titik P nol adalah besarnya medan listrik akibat Q1 besarnya sama dengan medan listrik akibat muatan Q2.
Dengan demikian, letak titik P adalah 10 cm di sebalh kiri muatan Q1.
Rekomendasi Artikel Lainnya:
- indonesia berada di titik pertemuan tiga lempeng… indonesia berada di titik pertemuan tiga lempeng litosfer disebut letak Indonesia berada di titik pertemuan tiga lempeng litosfer, yaitu lempeng Indo-Australia, lempeng Eurasia dan lempeng Pasifik, disebut letak secara geologis. Akibat dari letak geologis tersebut, Indonesia menjadi daerah yang rawan bencana gempa bumi dan tsunami.
- sebuah transformator digunakan untuk menaikkan… Pembahasan Jawaban yang tepat untuk pertanyaan tersebut adalah C. Diketahui: Ditanya: Jawab: Transformator atau disebut juga dengan trafo, adalah alat untuk mengubah tegangan listrik bolak balik (AC) yang memiliki dua kumparan yaitu kumparan primer dan kumparan sekunder. Menghitung kuat arus primer pada trafo: Pernyataan 1 salah. Menghitung kuat arus sekunder pada…
- jelaskan hubungan antara suprastruktur dan… jelaskan hubungan antara suprastruktur dan infrastruktur politik Memiliki hubungan dan kertertarikan secara struktur dan kedaulatan, Lembaga suprastruktur merupakan lembaga memiliki kedudukan lebih tinggi secara struktur dan secara kedaulatan lembaga suprastruktur merupakan bagian dari lembaga infrastruktur. Memiliki hubungan timbal balik, bentuk hubungan ini yaitu adanya hubungan salung ketergatungan antara lembaga…
- sebutkan tokoh protagonis dalam cerita berjudul… Pertanyaan Bacalah bacaan berikut! Caadara Panglima Wire adalah panglima perang dari Desa Kramuderu yang gagah berani. Panglima Wire mempunyai seorang putra bernama Caadara. Caadara kecil memiliki bakat dalam ilmu bela diri dan ketangkasan. Panglima Wire melatih Caadara dengan harapan Caadara dapat menggantikannya kelak. Caadara tumbuh menjadi pemuda tangkas dalam ilmu…
- Investasi Aset Kripto dengan Harga Rendah Selengkapnya tentang investasi aset kripto dengan harga rendah serta memahami alasan naik turunnya harga aset kripto di pasaran! Tren untuk membeli aset kripto kian meningkat dari waktu ke waktu. Sejalan dengan ini, eksistensi Bitcoin juga mendorong minat serta kepercayaan investor untuk membeli aset kripto. Dalam artikel ini akan dijelaskan…
- Pengadilan Menyita Aset Yang DiAgunkan Perintah pengadilan untuk menyita properti dari terdakwa untuk melunasi hutang dikenal sebagai Garnishment. Jenis Hukuman lainnya adalah otomatis memotong gaji debitur. Jika debitur gagal melunasi utangnya, pengadilan dapat memberinya pemotongan. Ketika pemberi pinjaman meminta pengadilan untuk mengirimkan sebagian dari gajinya untuk melunasi hutang dan tindakan ini diambil. Hukum dekorasi bervariasi…
- Komunitas keturunan Arab dengan masyarakat asli… A. Terjadinya amalgamasi antara komunitas keturunan Arab dengan masyarakat CondetB. keterbukaan dalam diri komunitas keturunan Arab dan masyarakat Condet asli terhadap agama lainC. kesediaan komunitas keturunan Arab menghormati dan menghargai orang asing dan kebudayaan yangdibawanya D. keinginan untuk menyeragamkan budaya kedua kelompok sehingga membentuk satu kebudayaan nasional bersama E. kesamaan agama dan…
- Jangan Buru-Buru Investasi, Pelajari Dulu Sebelum Tertipu Dikala ini banyak sekali ijab investasi yang tersebar di warga besar, tercantum yang terpaut dengan trading bagus saham, forex, kencana, kripto ataupun yang lain. Tetapi sayangnya tidak seluruh ijab investasi itu betul terdapatnya. Beberapa besar justru jadi pembohongan, scam, ataupun kerap diucap investasi bodong. Buat seperti itu aku menulis postingan…
- Apa yang Dilakukan Moderator Reddit? Subreddit berfungsi sebaik yang mereka lakukan berkat moderator sukarelawan. Tapi apa sebenarnya yang dilakukan moderator Reddit? Reddit, seperti kebanyakan komunitas online besar, memiliki moderator yang mengatur berbagai subredditnya. Namun, moderator komunitas ini tidak bekerja untuk perusahaan. Jadi apa yang dilakukan moderator Reddit dan jenis tanggung jawab apa yang mereka miliki…
- Penulisan tempat dan tanggal surat yang tepat adalah... Penulisan dari tempat dan juga tanggal dari surat yang dinilai tepat yaitu ialah dengan diawali menyebutkan sebuah tempat ataupun lokasi dari penulisannya. Kemudian, penulisan tanggal telah disesuaikan dengan waktu dari pembuatan surat tersebut. Penulisan dari tanggal ini dapat diawali dengan menuliskan tanggal, bulan, dan selanjutnya tahun. Contoh dari penulisan tempat dan juga tanggal yang benar yaitu ialah Semarang, 10 Maret 2021. Pembahasan Pengertian dari surat yaitu ialah sebuah sarana komunikasi…
- Pendekatan Untuk Memperoleh Ide Produk Hiasan… Pendekatan Untuk Memperoleh Ide Produk Hiasan Adalah.. Kecuali..... A. Siapa Calon Pembeli Dan Bagaimana Seleranya B. Eksplorasi Material Untuk Inovasi Estetik Baru C. Pikirkan Suatu Tempat Dan Hiasan Apa Yang Dibutuhkan Di Tempat Itu D. Berkunjung Ke Daerah Lain Dan Melihat Contoh Produk Kerajinan Hiasan E. Membuat Produk Kemudian Memasarkannya…
- Ini 5 Perbedaan Saham Syariah dan Saham Konvensional! Mau tanam saham tapi bingung jenis saham syariah atau konvensional? Pahami dulu perbedaan saham syariah dan saham konvensional. Ingin mencoba menanam saham, tapi bingung jenis saham mana yang akan dipilih, saham syariah atau konvensional? Maka dari itu, Anda harus tahu perbedaan saham syariah dan saham konvensional yang akan dijabarkan pada…
- terbentuknya pancasila sebagai pandangan hidup… 1. Makna Pancasila sebagai Dasar Negara dan Pandangan hidup artinya Pancasila dijadikan dasar dan motivasi dalam bersikap, tingkah laku, dan perbuatan dalam hidup bermasyarakat, berbangsa, dan bernegara. Pancasila dapat dikatan sebagai dasar negara, pandangan hidup, ideologi dan ligatur dalam kehidupan berbangsa dan kenegaraan Indonesia. 2. Pancasila disebut juga sebagai kepribadian…
- menentukan unsur unsur iklan slogan dan poster menentukan unsur unsur iklan slogan dan poster IKLAN Iklan adalah suatu pesan tentang barang atau jasa yang dibuat oleh pembuat barang yang disampaikan lewat media (cetak, audio, elektronik) yang di tujukan kepada masyarakat umum. Unsur - Unsur Iklan ⇒ Attention ( perhatian ). Iklan yang baik harus dapat menarik…
- 11 Catatan MUI Mengenai Halal Atau Haramnya Investasi Kripto Investasi aset kripto saat ini banyak diminati berbagai kalangan tak hanya di Indonesia, tapi juga di seluruh dunia. Nah pertanyaannya, investasi di aset kripto seperti Bitcoin itu halal atau haram, ya? Terkait hal ini, Majelis Ulama Indonesia (MUI) pernah memberi 11 catatan terkait aset kripto seperti bitcoin. Dalam catatan itu, disebutkan…
- Cara Mengatur Keungan Bagi Pasang Yang Baru Menikah Banyak pengantin baru yang merasa kesulitan untuk menyesuaikan diri dengan gaya hidup baru, terutama dalam hal keuangan. Sebagai orang yang berbeda, kebiasaan belanja Anda akan bervariasi. Itulah mengapa Anda berdua perlu melakukan beberapa penyesuaian untuk menutupi anggaran domestik Anda. Berikut beberapa cara yang bisa Anda dan pasangan lakukan untuk membuat…
- Produk Pasar Modal Syariah Yang Aman Dan Menarik Produk pasar modal syariah menjadi pilihan banyak orang dalam pencarian keuntungan. Ini pilihan mudah untuk dimanfaatkan. Pasar modal menjadi salah satu cara yang orang gunakan untuk mendapatkan banyak keuntungan. Anda dapat melakukan jual beli surat berharga dengan mudah dan mengikuti prinsip syariah. Jelas kalau Anda tidak boleh asal dalam pemilihan…
- berdasarkan data pada gambar kuat arus listrik i adalah Diketahui: Ditanyakan: I = ...? Pembahasan: Pada rangkaian listrik tertutup, kita dapat menentukan kuat arus yang mengalir dengan persamaan: Pada rangkaian hanya memiliki satu buah baterai dan tidak terdapat hambatan dalam maka: Akan tetapi, besar hambatan pengganti total perlu diketahui terlebih dahulu. Langkah pertama: menghitung hambatan pengganti Hambatan R2 dan R3 dipasang paralel,…
- 3 Biaya Rutin Yang Harus Dikeluarkan Ketika Membeli Mobil Apakah Anda tahu perbedaan antara mal dan jalan raya? Hanya ada satu jawaban. bagaimana? Cobalah pergi ke mal. Anda berinteraksi dengan item yang muncul di jendela toko. Cepat atau lambat Anda pasti ingin membeli salah satu barang tersebut, bukan? Sementara itu, jika Anda berada di jalan raya, Anda akan ditabrak…
- Mengenal Bagaimana Sistem Keuntungan Pada Asuransi Syariah Jika tertarik berinvestasi Anda bisa mencoba mendaftar asuransi syariah. Selain mendapat layanan asuransi Anda juga berkesempatan mendapat pembagian keuntungan asuransi syariah sebagaimana dijelaskan pada artikel ini. Jika tertarik untuk mendaftar asuransi secara halal serta akad yang jelas, Anda bisa coba asuransi syariah. Pembagian keuntungan asuransi syariah dilaksanakan secara merata antara…
- kelompok senyawa dibawah ini yang mempunyai ikatan… Pembahasan Ikatan ion adalah ikatan yang terjadi akibat perpindahan elektron dari satu atom ke atom lain. Ikatan ion terbentuk antara atom yang melepaskan elektron (logam) dengan atom yang menangkap elektron (bukan logam). Atom logam, setelah melepaskan elektron berubah menjadi ion positif. Sedangkan atom bukan logam, setelah menerima elektron berubah menjadi…
- Suku Tengger sebagai warga asli yang mendiami… Berdasarkan ilustrasi tersebut, analisis pendekatan fungsionalis yang berkaitan dengan stratifikasi sosial adalah .... A. pola perilaku masyarakat masih tradisional berdasarkan adat istiadat yang dipegang teguh B. ada dualisme kepemimpinan karena ketua adat dan dukun adat memiliki kewenangan yang sama C. kepemimpinan dalam suku Tengger hanya diperuntukkan kepada lapisan atas yang memiliki kompetensi D.…
- pernyataan berikut yang menyatakan reaksi orde nol adalah Pembahasan Orde merupakan pangkat dari konsentrasi, sehingga ketika orde nol, artinya konsentrasi berpangkat nol, maka pengali reaksinya adalah nol, sehingga perubahan konsentrasi tidak ada pengaruhnya terhadap laju reaksi.
- Tidak Perlu Panik, Ikuti 3 Cara Atasi Kartu Kredit Diblokir Cara atasi kartu kredit diblokir menjadi hal penting untuk banyak orang. Anda dapat menggunakan cara ini jika kartu tidak dapat digunakan. Kartu kredit menjadi salah satu jenis kartu yang penting untuk banyak orang. Pasalnya, kartu ini dapat memberikan kemudahan untuk semua pengguna. Anda dapat memperoleh efisiensi dalam transaksi hingga menghemat…
- sebuah bola konduktor berjari jari 10 cm Diketahui: R = 10 cm = 0,1 m q = 10-9 C k = 9 × 109 Nm2C-2 r = 9 cm = 0,09 m Ditanya: E = ...? dan V = ...? Jawaban: Kita anggap bola yang dimaksud disini adalah bola konduktor berongga. Ketika bola konduktor berongga diberi muatan listrik,…
- Produk Jasa Perbankan Yang Mungkin Belum Anda Ketahui Perlu anda ketahui Pelayanan Perbankan Tidak hanya menyediakan produk simpanan dan kredit, namun ada beberapa produk perbankan lainnya seperti juga menyediakan layanan jasa lainnya untuk memudahkan transaksi keuangan nasabah baik untuk kebutuhan bisnis maupun personal. Lalu apa saja produk Perbankan yang mungkin blm anda ketahui??? Surat Kredit Berdokumen (Letter of…
- Asuransi Syariah VS Asuransi Konvensional, Mana Yang… Penggunaan asuransi bagi kehidupan manusia memang penting dan krusial. Pun faktor ini juga mempengaruhi tahapan kebebasan finansial bagi kehidupan setiap orang. Banyaknya aktivitas perbankan baik secara konvensional hingga berbasis syariah sering Anda temui penawarannya. Kali ini Anda akan membaca ulasan tentang asuransi syariah vs asuransi konvensional. Pembahasan ini tidak akan…
- 4 Tips Sebelum Memutuskan Menggunakan Kartu Kredit… Kartu kredit menjadi pilihan banyak orang untuk kemudahan dalam berbelanja. Anda dapat membuat kartu untuk belanja dengan bebas. Cara ini bahkan dianggap sebagai healing untuk beberapa orang yang suka belanja. Beberapa orang lainnya memilih membuat kartu untuk belanja kebutuhan yang dapat dicicil. Anda perlu tips sebelum memutuskan menggunakan kartu kredit.…
- perhatikan gambar dibawah ini m adalah titik tengah qr Untuk membuktikan , perhatikan kembali gambar . Perhatikan bahwa QM = MR (memiliki tanda yang sama). XM = YM (diketahui dari soal). Pada kedua segitiga terdapat sudut siku-siku, maka berlaku teorema pythagoras. Kita hitung sisi XQ pada , maka: Perhatikan pun demikian, berlaku teorema pythagoras ,kita hitung sisi YR: Karena QM = MR dan XM = YM…
- Ketika Hati Harus Mengalah Cerpen Karangan : Elsa ArifiyantiAlamat : Jalan Ahmad Dahlan, RT 02/RW 05 Jengglong, Kel. Kaweron, Kec.Talun, Kab. Blitar Reta adalah anak yang aktif di Organisasi, selain aktif dia juga memiliki paras yang anggun dan berhati mulia.Dengan berOrganisasi Reta menemukan sosok sahabat yang baik dan mau mendengarkan semua keluh kesah Reta. Yaa,…
- Peluang Investasi Emas Digital yang Memberikan… Sebelum beralih investasi ke emas digital maka perlu mengetahui peluang investasi emas digital yang banyak memberikan keuntungan, yuk simak ulasannya berikut ini! Sejak adanya pandemi masyarakat mulai melirik keuntungan dari investasi emas digital yang dinilai memiliki banyak manfaat dan kelebihan. Salah satunya emas digital dinilai lebih aman karena memiliki…
- besar kuat medan listrik dititik a adalah Pembahasan Diketahui : Ditanya : Muatan positif memiliki medan yang arahnya keluar, sedangkan muatan negatif memiliki medan listrik yang arahnya masuk. Sehingga titik A mengalami dua medan listrik dengan arah seperti gambar Kuat medan di titik A dapat dihitung menggunakan persamaan Jadi, jawaban yang tepat adalah B.
- jelaskan perbedaan kata dan istilah perbedaan antara kata dan istilah adalah kata dapat bermakna ganda karena makna kata sesuai dengan konsep kalimat, sedangkan istilah tidak bermakna ganda karena diungkapkan dengan kata yang khusus untuk konsep tersebut. Definisi kata Definisi kata adalah penjelasan tentang makna atau arti kata tertentu yang dijelaskan secara leksikal, semantik, dan pragmatik.…
- Rekomendasi Investasi Murah untuk Milenial Investasi Murah untuk Milenial Anda seorang milenial yang ingin memulai investasi? Jangan lewatkan informasi tentang investasi murah untuk milenial berikut ini! Investasi saat ini mulai banyak dilirik oleh para milenial. Karena perkembangan zaman, saat ini investasi dapat dengan mudah dilakukan. Selain itu, Anda dapat memulai investasi dengan modal yang sangant…
- sistem organ dan organ penyusunnya sistem organ dan organ penyusunnya Organ penyusun: 1. Hidung, berfungsi untuk enyaring, mengatur suhu, dan melembabkan udara yang masuk. 2. Faring, berfungsi menyediakan saluran bagi udara yang keluar masuk. 3. Tenggorokan, berfungsi menyaring udara yang kita hirup dan juga bercabang ke bronkus. 4. Paru-paru, terdapat alveolus yang berfungsi menukar…
- tabel perbedaan pembuluh darah arteri dan vena Pembuluh darah merupakan serangkaian tabung (saluran) tertutup dan bercabang yang berfungsi membawa darah dari jantung ke jaringan, kemudian kembali ke jantung. Pembuluh darah utama ada tiga macam, yaitu arteri, kapiler, dan vena. Arteri berfungsi untuk membawa darah meninggalkan jantung. Kapiler merupakan pembuluh darah yang sangat halus dan berdinding sangat tipis…
- perhatikan gambar model atom berikut Gambar model atom diatas merupakan Teori Atom Thomson. Thomson mengusulkan teori atom sebegai berikut : Atom merupakan bola pejal yang memiliki muatan positif. Elektron yang bermuatan negatif tersebar di dalamnya. Jumlah muatan positif sama dengan jumlah muatan negatif sehingga atom bersifat netral. Berdasarkan penjelasan di atas, pernyataan yang tepat adalah…
- Inilah 5 Cara Bank Menentukan Limit Kredit Pengguna! Limit kredit adalah adalah jumlah maksimum yang diberikan oleh sebuah Bank kepada pengguna debitur. Tentu saja Bank memiliki caranya sendiri dalam menentukan limitnya. Lalu bagaimana cara Bank menentukan limit kredit pengguna? Berikut ini akan kami jelaskan. Inilah Cara Bank Menentukan Limit Kredit Pengguna Ada beberapa faktor yang dilihat oleh Bank…
- Teks negosiasi berikut yang termasuk bagian… Teks negosiasi berikut yang termasuk bagian persetujuan adalah.... Anak: Uang sya tidak cukup, bagaimana kalo Rp.48.000,00 Saja? Penjaga: itu terlalu murah, bagimana kalau Rp.55.000,00 saja? B. Anak: Tapi uang saya hanya Rp50.000,00. Penjaga: Begini saja, saya akan berikan bku ini seharga Rp.50.000.00. Bagimana? Anak: Baiklah, Pak! Saya beli bukunya. Penjaga:…
- Berikan 3 (tiga) contoh perwujudan kerjasama dalam… Dalam lingkungan masyarakat, berikut adalah beberapa contoh dari perwujudan kerja sama yang bisa dilakukan: Kerja sama melakukan ronda malam untuk mencegah kejahatan. Kerja sama untuk membersihkan lingkungan dengan kerja bakti. Kerja sama untuk memperbaiki jalan. Pembahasan Kerja sama adalah upaya yang dilakukan oleh beberapa pihak sekaligus untuk mencapai suatu tujuan bersama. Kerja sama juga menjadi…
- berikut yang bukan merupakan langkah-langkah menulis resensi berikut yang bukan merupakan langkah-langkah menulis resensi Dalam menulis resensi, yang bukan termasuk langkah-langkah menulis ialah menaksir harga buku. Resensi merupakan suatu kegiatan menilai, membahas, mengkritik dan mengungkapkan kembali isi yang terdapat dalam sebuah karya sastra.
- Apa Saja Premi Asuransi Syariah???? Yuk Kenali Jenis… Tidak jauh berbeda dengan premi asuransi konvensional, Asuransi syariah juga memiliki empat jenis premi, Misalnya seperi asuransi jiwa, kesehatan, dan sebagainya. Apa Yang Dimaksud Dengan Premi Syariah?? Premi asuransi syariah adalah dana kontribusi yang dihibahkan oleh nasabah untuk saling menanggung risiko Nantinya, dana kontribusi itu dikelola oleh perusahaan asuransi yang…
- Lebih Baik Reksadana atau Saham? Mungkin ada sebagian dari Anda yang masih merasa ragu, mengenai lebih baik reksadana atau saham? Untuk itu, yuk simak terlebih dahulu informasi di bawah ini! Bagi Anda yang baru akan memulai investasi, pastinya ada banyak pilihan investasi yang mungkin hal ini malah membuat Anda bingung, mengenai mana yang harus Anda…
- Kolom neraca saldo disesuaikan dalam kertas kerja berisi... Dalam sebuah perusahaan, adanya laporan keuangan menjadi salah satu hal yang terpenting untuk bisa mengetahui bagaimana siklus keuangan dari perusahaan tersebut. Dengan membuat sebuah catatan keuangan yang rapi, tenu akan mempermudah dalam melakukan analisis dan evaluasi. Salah satu laporan keuangan yang terbilang penting yaitu neraca lajur Keberadaan neraca yang…
- Arus globalisasi terkadang berdampak negatif bagi… Upaya yang dapat dilakukan untuk mengatasi masalah sosial tersebut adalah …. A. meyakinkan generasi muda bahwa agama dan kehidupan moral dunia dapat berjalan berseberangan, tanpa harus menghasilkan konflik di dalam kehidupan masyarakat B. mendorong lembaga agama untuk menguatkan kembali perannya dalam memberikan identitas keagamaan dan peningkatan kontrol sosial kepada masyarakat C. memperkuat…
- Yuk, Ikuti 4 Cara Agar Tagihan Kartu Kredit Tidak Jebol Untuk mendapatkan kemudahan agar tidak rugi. Maka, Anda dapat menggunakan cara agar tagihan kartu kredit tidak jebol. Menggunakan kartu kredit adalah hal yang menarik untuk banyak orang. Anda dapat memanfaatkan kartu ini untuk kemudahan sendiri. Banyak cara menarik untuk melakukan pembayaran dengan mudah. Anda dapat menggunakan kartu sebagai pilihan…
- kegunaan zat aditif nama zat aditif dampak negatif… Pembahasan: Nama-nama zat aditif serta dampak negatif dan pencegahannya: 1. Penguat rasa Contoh penguat rasa adalah monosodium glutamat, atau MSG. Dampak penggunan MSG banyak diperdebatkan, beberapa menganggap bahwa MSG menyebabkan efek samping seperti alergi, dan denyut jantung yang tak teratur. Namun sebagian besar ilmuwan tidak menganggap MSG berbahaya. Bila ingin…
- diketahui kubus abcd efgh dengan panjang rusuk 12 Gunakan konsep menentukan jarak antara titik ke garis. Agar lebih mudah hubungkan titik ke diagonal sisi menjadi seperti berikut. Kemudian pisahkan segitiga yang terbentuk tersebut yaitu , karena , dan merupakan diagonal sisi, maka panjangnya sama sehingga membentuk segitiga sama sisi. Untuk menentukan jarak titik ke diagonal sisi , dengan menarik garis tegak lurus dengan dan membagi dua sisi , jika digambarkan…
- nilai kuartil bawah dari data tersebut adalah Pembahasan Perhatikan perhitungan berikut. Ingat: menentukan letak kelas kuartil rumus menghitung kuartil dengan: adalah tepi bawah kelas kuartil adalah frekuensi kumulatif sebelum kelas kuartil ke- adalah frekuensi kelas kuartil ke- adalah panjang kelas adalah banyak data Maka: Kelas kuartil bawah atau kuartil ke-1 yaitu: Jadi, kelas kuartil bawah atau kuartil ke-1…
- tabel perbedaan arteri dan vena Pembuluh darah merupakan serangkaian tabung (saluran) tertutup dan bercabang yang berfungsi membawa darah dari jantung ke jaringan, kemudian kembali ke jantung. Pembuluh darah utama ada tiga macam, yaitu arteri, kapiler, dan vena. Arteri berfungsi untuk membawa darah meninggalkan jantung. Kapiler merupakan pembuluh darah yang sangat halus dan berdinding sangat tipis…
 AINU Media AINU Media Memberikan Informasi Terpercaya dan Terupdate
AINU Media AINU Media Memberikan Informasi Terpercaya dan Terupdate